Statistics - Venn Diagram

---

---

Venn diagram is a way to visually represents relationship between groups of entities or objects. Venn diagrams are comprised of circles where each circle represents a whole set. Venn diagram can have unlimited circles but generally two or three circles are preferred otherwise the diagram becomes too complex.

Steps to draw a Venn Diagram

Consider the following sets of people:

1. Cricket Players - $ C = \{ Ram, Shyam, Mohan, Rohan, Ramesh, Suresh \} $

2. Hockey Players - $ H = \{ Ramesh, Naresh, Mahesh, Leela, Sunita \} $

Step 1: Draw a rectangle and label it as players.

Step 2: Draw two circles and label them as Cricket and Hockey. Make sure that circles are overlapping each other.

Step 3: Write Names inside the circle as relevant. Common name(s) should fall within common region.

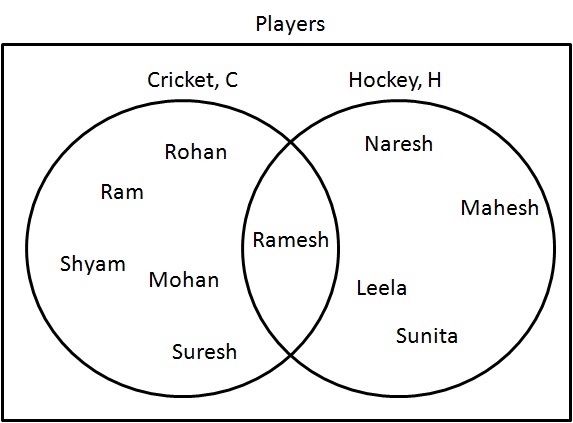
Union

Union ($ \cup $) represents a set where items are present in all categories but are not repeated.

Example

Problem Statement:

Draw a Venn diagram of $ C \cup H $.

Solution:

Step 1: Determine players who are either playing cricket or hockey. Draw them as following:

$ C \cup H = \{ Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.

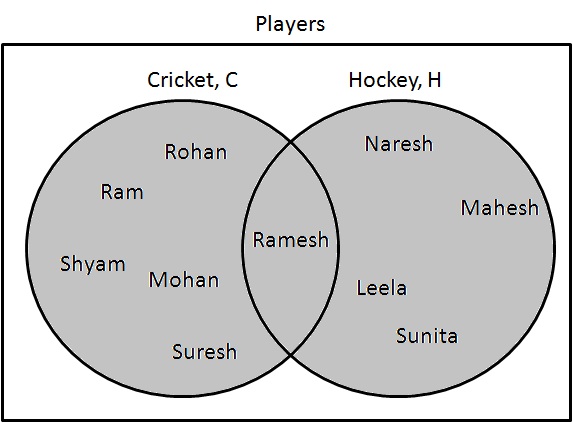
Intersection

Intersection ($ \cap $) represents a set where items are present in both categories.

Example

Problem Statement:

Draw a Venn diagram of $ C \cap H $.

Solution:

Step 1: Determine players who are playing cricket and hockey both. Draw them as following:

$ C \cap H = \{ Ramesh \} $.

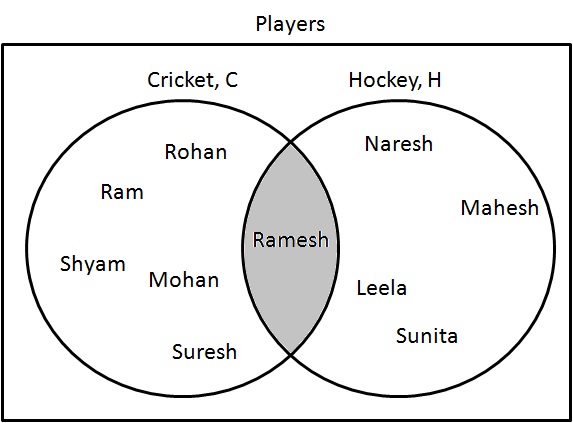
Difference

Difference ($ - $) represents a set where items are present only in one category and not in other one.

Example

Problem Statement:

Draw a Venn diagram of $ C - H $.

Solution:

Step 1: Determine players who are playing cricket only. Draw them as following:

$ C - H = \{ Ram, Shyam, Mohan, Rohan, Suresh \} $.