SciPy - Spatial

---

---

The scipy.spatial package can compute Triangulations, Voronoi Diagrams and Convex Hulls of a set of points, by leveraging the Qhull library. Moreover, it contains KDTree implementations for nearest-neighbor point queries and utilities for distance computations in various metrics.

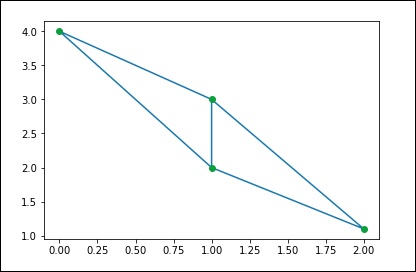
Delaunay Triangulations

Let us understand what Delaunay Triangulations are and how they are used in SciPy.

What are Delaunay Triangulations?

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P).

We can the compute the same through SciPy. Let us consider the following example.

from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

The above program will generate the following output.

Coplanar Points

Let us understand what Coplanar Points are and how they are used in SciPy.

What are Coplanar Points?

Coplanar points are three or more points that lie in the same plane. Recall that a plane is a flat surface, which extends without end in all directions. It is usually shown in math textbooks as a four-sided figure.

Let us see how we can find this using SciPy. Let us consider the following example.

from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar

The above program will generate the following output.

array([[4, 0, 3]], dtype = int32)

This means that point 4 resides near triangle 0 and vertex 3, but is not included in the triangulation.

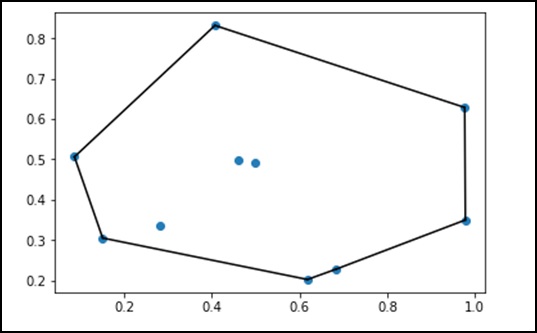
Convex hulls

Let us understand what convex hulls are and how they are used in SciPy.

What are Convex Hulls?

In mathematics, the convex hull or convex envelope of a set of points X in the Euclidean plane or in a Euclidean space (or, more generally, in an affine space over the reals) is the smallest convex set that contains X.

Let us consider the following example to understand it in detail.

from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

The above program will generate the following output.