Python - Set Operators

---

---

Set Operators in Python

The set operators in Python are special symbols and functions that allow you to perform various operations on sets, such as union, intersection, difference, and symmetric difference. These operators provide a way to combine, compare, and modify sets.

Python implements them with following set operators −

Python Set Union Operator (|)

The union of two sets is a set containing all distinct elements that are in A or in B or both. For example,

{1,2}∪{2,3}={1,2,3}

The following diagram illustrates the union of two sets.

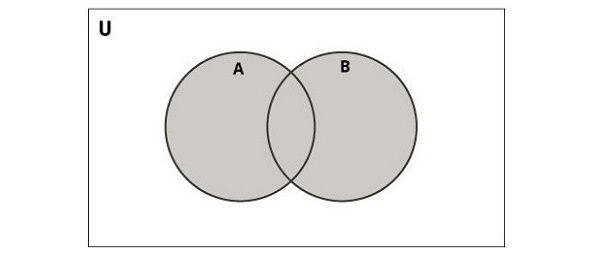
In Python, you can perform the union operation using the union() function or the | operator. This operation combines the elements of two sets while eliminating duplicates, resulting in a new set containing all unique elements from both sets −

Example

The following example uses the "|" operator and union() function, and returns the union of two sets −

set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 45, 73}
union_set1 = set1.union(set2)
union_set2 = set3 | set4
print ('The union of set1 and set2 is', union_set1)
print ('The union of set3 and set4 is', union_set2)

After executing the above code, we get the following output −

The union of set1 and set2 is {1, 2, 3, 4, 5}
The union of set3 and set4 is {73, 6, 8, 9, 45}

Python Set Intersection Operator (&)

The intersection of two sets AA and BB, denoted by A∩B, consists of all elements that are common to both in A and B. For example,

{1,2}∩{2,3}={2}

The following diagram illustrates intersection of two sets.

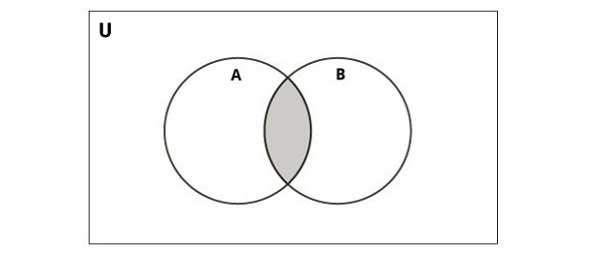
Python provides the intersection() function or the & operator to perform this operation. The resulting set contains only the elements present in both sets −

Example

Following example uses & operator and intersection() function, and returns intersection of two sets −

set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
intersection_set1 = set1.intersection(set2)  
intersection_set2 = set3  & set4
print ('The intersection of set1 and set2 is', intersection_set1)
print ('The intersection of set3 and set4 is', intersection_set2)

It will produce the following output −

The intersection of set1 and set2 is {3}
The intersection of set3 and set4 is {8, 9}

Python Set Difference Operator (-)

The difference (subtraction) between two sets consists of elements present in the first set but not in the second set. It is defined as follows. The set A−B consists of elements that are in A but not in B. For example,

If A={1,2,3} and B={3,5}, then A−B={1,2}

The following diagram illustrates difference of two sets −

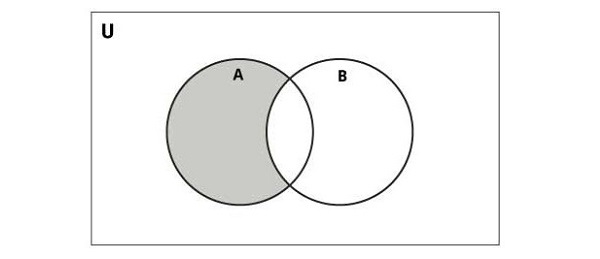
Python provides the difference() function or the - operator to perform this operation. The resulting set contains elements unique to the first set −

Example

The following example uses the "-" operator and the difference() function, and returns difference of two sets −

set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
difference_set1 = set1.difference(set2)
difference_set2 = set3 - set4
print ('The difference between set1 and set2 is', difference_set1)
print ('The difference between set3 and set4 is', difference_set2)

We get the output as shown below −

The difference between set1 and set2 is {1, 2}
The difference between set3 and set4 is {6}

Note that "s1-s2" is not the same as "s2-s1".

Python Set Symmetric Difference Operator

The symmetric difference of two sets consists of elements that are present in either set but not in both sets. The symmetric difference of A and B is denoted by "A Δ B" and is defined by −

A Δ B = (A − B) ⋃ (B − A)

If A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {1, 3, 5, 6, 7, 8, 9}, then A Δ B = {2, 4, 9}.

The following diagram illustrates the symmetric difference between two sets −

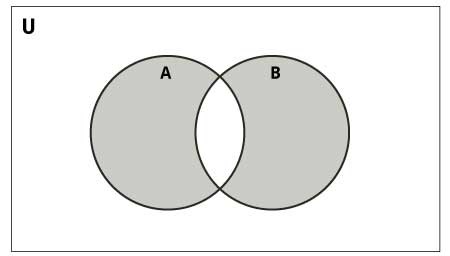
Python provides the symmetric_difference() function or the ^ operator to perform this operation. The resulting set contains elements that are unique to each set.

Example

The following example uses the "^" operator and the symmetric_difference() function, and returns symbolic difference of two sets −

set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
symmetric_difference_set1 = set1.symmetric_difference(set2)  
symmetric_difference_set2 = set3 ^ set4
print ('The symmetric difference of set1 and set2 is', symmetric_difference_set1)
print ('The symmetric difference of set3 and set4 is', symmetric_difference_set2)

The result produced is as follows −

The symmetric difference of set1 and set2 is {1, 2, 4, 5}
The symmetric difference of set3 and set4 is {73, 6}

Python Subset Testing Operation

You can check whether one set is a subset of another using the issubset() function or the <= operator. A set A is considered a subset of another set B if all elements of A are also present in B −

Example

The following example uses the "<=" operator and the issubset() function, and returns subset testing of two sets −

set1 = {1, 2}
set2 = {1, 2, 3, 4}
set3 = {64, 47, 245, 48}
set4 = {64, 47, 3}
is_subset1 = set1.issubset(set2)  
is_subset2 = set3 <= set4
print ('set1 is a subset of set2:', is_subset1)
print ('set3 is a subset of set4:', is_subset2)

The result produced is as follows −

set1 is a subset of set2: True
set3 is a subset of set4: False