
- Natural Language Processing Tutorial
- NLP - Home
- NLP - Introduction
- NLP - Linguistic Resources
- NLP - Word Level Analysis
- NLP - Syntactic Analysis
- NLP - Semantic Analysis
- NLP - Word Sense Disambiguation
- NLP - Discourse Processing
- NLP - Part of Speech (PoS) Tagging
- NLP - Inception
- NLP - Information Retrieval
- NLP - Applications of NLP
- NLP - Python
- Natural Language Processing Resources
- NLP - Quick Guide
- NLP - Useful Resources
- NLP - Discussion
NLP - Word Level Analysis
In this chapter, we will understand world level analysis in Natural Language Processing.
Regular Expressions
A regular expression (RE) is a language for specifying text search strings. RE helps us to match or find other strings or sets of strings, using a specialized syntax held in a pattern. Regular expressions are used to search texts in UNIX as well as in MS WORD in identical way. We have various search engines using a number of RE features.
Properties of Regular Expressions
Followings are some of the important properties of RE −
American Mathematician Stephen Cole Kleene formalized the Regular Expression language.
RE is a formula in a special language, which can be used for specifying simple classes of strings, a sequence of symbols. In other words, we can say that RE is an algebraic notation for characterizing a set of strings.
Regular expression requires two things, one is the pattern that we wish to search and other is a corpus of text from which we need to search.
Mathematically, A Regular Expression can be defined as follows −
ε is a Regular Expression, which indicates that the language is having an empty string.
φ is a Regular Expression which denotes that it is an empty language.
If X and Y are Regular Expressions, then
X, Y
X.Y(Concatenation of XY)
X+Y (Union of X and Y)
X*, Y* (Kleen Closure of X and Y)
are also regular expressions.
If a string is derived from above rules then that would also be a regular expression.
Examples of Regular Expressions
The following table shows a few examples of Regular Expressions −
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | {0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | {ε, 0, 1, 01} |
| (a+b)* | It would be set of strings of a’s and b’s of any length which also includes the null string i.e. {ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | It would be set of strings of a’s and b’s ending with the string abb i.e. {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | It would be set consisting of even number of 1’s which also includes an empty string i.e. {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | It would be set of strings consisting of even number of a’s followed by odd number of b’s i.e. {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | It would be string of a’s and b’s of even length that can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null i.e. {aa, ab, ba, bb, aaab, aaba, …………..} |
Regular Sets & Their Properties
It may be defined as the set that represents the value of the regular expression and consists specific properties.
Properties of regular sets
If we do the union of two regular sets then the resulting set would also be regula.
If we do the intersection of two regular sets then the resulting set would also be regular.
If we do the complement of regular sets, then the resulting set would also be regular.
If we do the difference of two regular sets, then the resulting set would also be regular.
If we do the reversal of regular sets, then the resulting set would also be regular.
If we take the closure of regular sets, then the resulting set would also be regular.
If we do the concatenation of two regular sets, then the resulting set would also be regular.
Finite State Automata
The term automata, derived from the Greek word "αὐτόματα" meaning "self-acting", is the plural of automaton which may be defined as an abstract self-propelled computing device that follows a predetermined sequence of operations automatically.
An automaton having a finite number of states is called a Finite Automaton (FA) or Finite State automata (FSA).
Mathematically, an automaton can be represented by a 5-tuple (Q, Σ, δ, q0, F), where −
Q is a finite set of states.
Σ is a finite set of symbols, called the alphabet of the automaton.
δ is the transition function
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
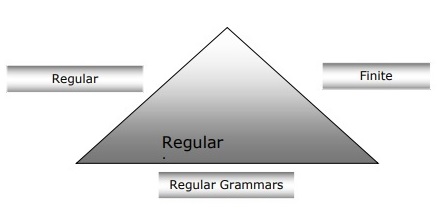
Relation between Finite Automata, Regular Grammars and Regular Expressions
Following points will give us a clear view about the relationship between finite automata, regular grammars and regular expressions −
As we know that finite state automata are the theoretical foundation of computational work and regular expressions is one way of describing them.
We can say that any regular expression can be implemented as FSA and any FSA can be described with a regular expression.
On the other hand, regular expression is a way to characterize a kind of language called regular language. Hence, we can say that regular language can be described with the help of both FSA and regular expression.
Regular grammar, a formal grammar that can be right-regular or left-regular, is another way to characterize regular language.
Following diagram shows that finite automata, regular expressions and regular grammars are the equivalent ways of describing regular languages.
Types of Finite State Automation (FSA)
Finite state automation is of two types. Let us see what the types are.
Deterministic Finite automation (DFA)
It may be defined as the type of finite automation wherein, for every input symbol we can determine the state to which the machine will move. It has a finite number of states that is why the machine is called Deterministic Finite Automaton (DFA).
Mathematically, a DFA can be represented by a 5-tuple (Q, Σ, δ, q0, F), where −
Q is a finite set of states.
Σ is a finite set of symbols, called the alphabet of the automaton.
δ is the transition function where δ: Q × Σ → Q .
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
Whereas graphically, a DFA can be represented by diagraphs called state diagrams where −
The states are represented by vertices.
The transitions are shown by labeled arcs.
The initial state is represented by an empty incoming arc.
The final state is represented by double circle.
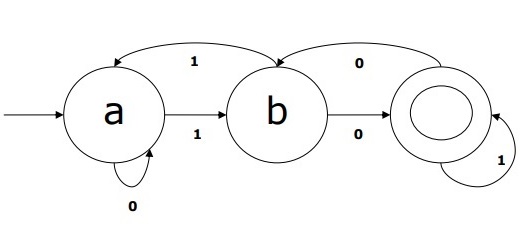
Example of DFA
Suppose a DFA be
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
Transition function δ is shown in the table as follows −
| Current State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| A | a | B |
| B | b | A |
| C | c | C |
The graphical representation of this DFA would be as follows −
Non-deterministic Finite Automation (NDFA)
It may be defined as the type of finite automation where for every input symbol we cannot determine the state to which the machine will move i.e. the machine can move to any combination of the states. It has a finite number of states that is why the machine is called Non-deterministic Finite Automation (NDFA).
Mathematically, NDFA can be represented by a 5-tuple (Q, Σ, δ, q0, F), where −
Q is a finite set of states.
Σ is a finite set of symbols, called the alphabet of the automaton.
δ :-is the transition function where δ: Q × Σ → 2 Q.
q0 :-is the initial state from where any input is processed (q0 ∈ Q).
F :-is a set of final state/states of Q (F ⊆ Q).
Whereas graphically (same as DFA), a NDFA can be represented by diagraphs called state diagrams where −
The states are represented by vertices.
The transitions are shown by labeled arcs.
The initial state is represented by an empty incoming arc.
The final state is represented by double circle.
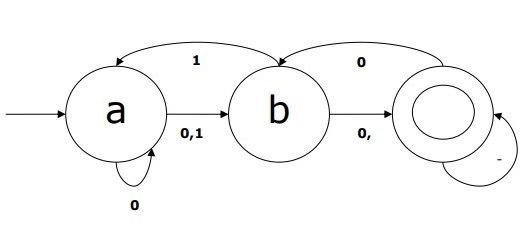
Example of NDFA
Suppose a NDFA be
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
Transition function δ is shown in the table as follows −
| Current State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| A | a, b | B |
| B | C | a, c |
| C | b, c | C |
The graphical representation of this NDFA would be as follows −
Morphological Parsing
The term morphological parsing is related to the parsing of morphemes. We can define morphological parsing as the problem of recognizing that a word breaks down into smaller meaningful units called morphemes producing some sort of linguistic structure for it. For example, we can break the word foxes into two, fox and -es. We can see that the word foxes, is made up of two morphemes, one is fox and other is -es.
In other sense, we can say that morphology is the study of −
The formation of words.
The origin of the words.
Grammatical forms of the words.
Use of prefixes and suffixes in the formation of words.
How parts-of-speech (PoS) of a language are formed.
Types of Morphemes
Morphemes, the smallest meaning-bearing units, can be divided into two types −
Stems
Word Order
Stems
It is the core meaningful unit of a word. We can also say that it is the root of the word. For example, in the word foxes, the stem is fox.
Affixes − As the name suggests, they add some additional meaning and grammatical functions to the words. For example, in the word foxes, the affix is − es.
Further, affixes can also be divided into following four types −
Prefixes − As the name suggests, prefixes precede the stem. For example, in the word unbuckle, un is the prefix.
Suffixes − As the name suggests, suffixes follow the stem. For example, in the word cats, -s is the suffix.
Infixes − As the name suggests, infixes are inserted inside the stem. For example, the word cupful, can be pluralized as cupsful by using -s as the infix.
Circumfixes − They precede and follow the stem. There are very less examples of circumfixes in English language. A very common example is ‘A-ing’ where we can use -A precede and -ing follows the stem.
Word Order
The order of the words would be decided by morphological parsing. Let us now see the requirements for building a morphological parser −
Lexicon
The very first requirement for building a morphological parser is lexicon, which includes the list of stems and affixes along with the basic information about them. For example, the information like whether the stem is Noun stem or Verb stem, etc.
Morphotactics
It is basically the model of morpheme ordering. In other sense, the model explaining which classes of morphemes can follow other classes of morphemes inside a word. For example, the morphotactic fact is that the English plural morpheme always follows the noun rather than preceding it.
Orthographic rules
These spelling rules are used to model the changes occurring in a word. For example, the rule of converting y to ie in word like city+s = cities not citys.