Matplotlib - Box Plots

A box plot represents the distribution of a dataset in a graph. It displays the summary statistics of a dataset, including the minimum, first quartile (Q1), median (Q2), third quartile (Q3), and maximum. The box represents the interquartile range (IQR) between the first and third quartiles, while whiskers extend from the box to the minimum and maximum values. Outliers, if present, may be displayed as individual points beyond the whiskers.

Imagine you have the exam scores of students from three classes. A box plot is a way to show how these scores are spread out −

Minimum and Maximum − The smallest and largest scores are shown as the ends of the plot.
Quartiles (Q1, Q2, Q3) − The scores are split into four parts. The middle score is the median (Q2). The scores below the median are the first quartile (Q1), and those above are the third quartile (Q3). It helps you see where most of the scores lie.
Interquartile Range (IQR) − The range between Q1 and Q3 is called the interquartile range.
Box − The box in the middle represents the interquartile range. So, it is showing you where half of the scores are.
Whiskers − Lines (whiskers) extend from the box to the smallest and largest scores, helping you see how spread out the scores are.
Outliers − If there are any scores way above or below the rest, they might be shown as dots beyond the whiskers. These are like the standout scores.

Box Plot in Matplotlib

We can create a box plot in Matplotlib using the boxplot() function. This function allows us to customize the appearance of the box plot, such as changing the whisker length, adding notches, and specifying the display of outliers.

The boxplot() Function

The boxplot() function in Matplotlib takes one or more datasets as input and generates a box plot for each dataset.

Following is the syntax of boxplot() function in Matplotlib −

Syntax

plt.boxplot(x, notch=None, patch_artist=None, widths=None, labels=None, ...)

Where,

x is the dataset or a list of datasets for which the box plot is to be created.
If notch (optional) is True, it creates a vertical box plot; if False, creates a horizontal box plot.
If patch_artist (optional) is True, it fills the box with color.
widths (optional) represents the width of the boxes.
labels (optional) sets labels for each dataset, useful when plotting multiple box plots.

These are just a few parameters; there are more optionals parameters available for customization.

Horizontal Box Plot with Notches

We can create a horizontal box plot with notches to display the distribution of a dataset in a horizontal orientation. It includes notches around the median lines, providing a visual estimate of the uncertainty around the median values.

Example

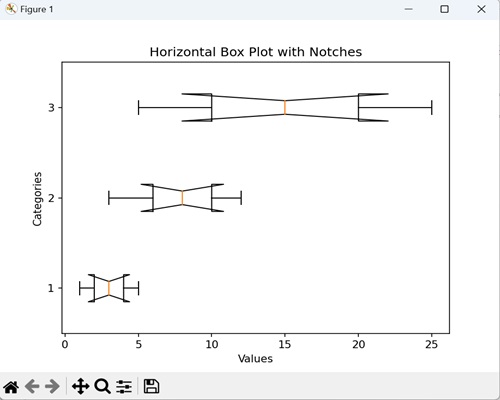
In the following example, we are creating a horizontal box plot with notches around the medians for three data sets, where each box represents a set of values along the y-axis categories −

import matplotlib.pyplot as plt

# Data
data = [[1, 2, 3, 4, 5], [3, 6, 8, 10, 12], [5, 10, 15, 20, 25]]

# Creating a horizontal box plot with notches
plt.boxplot(data, vert=False, notch=True)
plt.title('Horizontal Box Plot with Notches')
plt.xlabel('Values')
plt.ylabel('Categories')
plt.show()

Output

After executing the above code, we get the following output −

Box Plot with Custom Colors

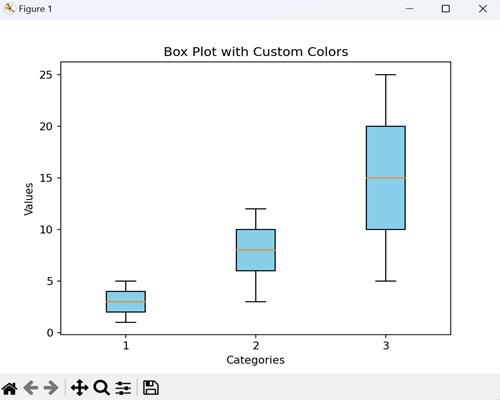
We can create a box plot with custom colors, graphically representing the data with different colors to fill the boxes. Each box represents the distribution of values within a category, and by adding a custom color, we introduce a stylistic touch that makes it easier to differentiate between categories.

Example

In here, we are enhancing the box plot by filling the boxes with a custom color i.e. skyblue −

import matplotlib.pyplot as plt
data = [[1, 2, 3, 4, 5], [3, 6, 8, 10, 12], [5, 10, 15, 20, 25]]

# Creating a box plot with custom colors
plt.boxplot(data, patch_artist=True, boxprops=dict(facecolor='skyblue'))
plt.title('Box Plot with Custom Colors')
plt.xlabel('Categories')
plt.ylabel('Values')
plt.show()

Output

Following is the output of the above code −

Grouped Box Plot

We can create a grouped box plot to compare the distributions of multiple groups side by side. Each group has its own set of boxes, where each box represents the distribution of values within that group.

Example

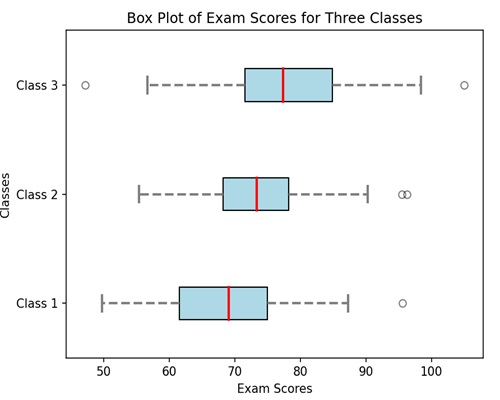
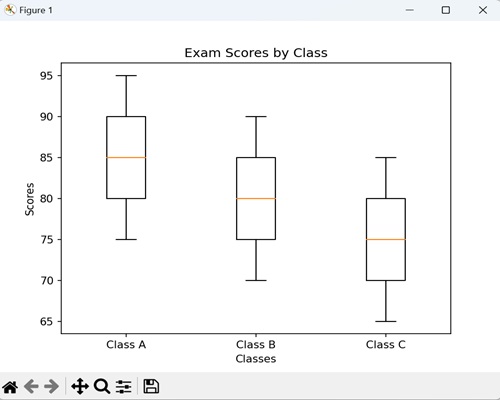
Now, we are creating a grouped box plot to compare the exam scores of students from three different classes (A, B, and C). Each box represents the distribution of scores within a class, allowing us to easily observe and compare the central tendencies, spreads, and potential outliers across the three classes −

import matplotlib.pyplot as plt
import numpy as np
class_A_scores = [75, 80, 85, 90, 95]
class_B_scores = [70, 75, 80, 85, 90]
class_C_scores = [65, 70, 75, 80, 85]

# Creating a grouped box plot
plt.boxplot([class_A_scores, class_B_scores, class_C_scores], labels=['Class A', 'Class B', 'Class C'])
plt.title('Exam Scores by Class')
plt.xlabel('Classes')
plt.ylabel('Scores')
plt.show()

Output

On executing the above code we will get the following output −

Box Plot with Outliers

A box plot with outliers is a graphical representation of data that includes additional information about extreme values in the dataset. In a standard box plot, we represent outliers, data points significantly different from the majority, as individual points beyond the "whiskers" that extend from the box.

This plot helps in identifying exceptional values that may have a significant impact on the overall distribution of the data.

Example

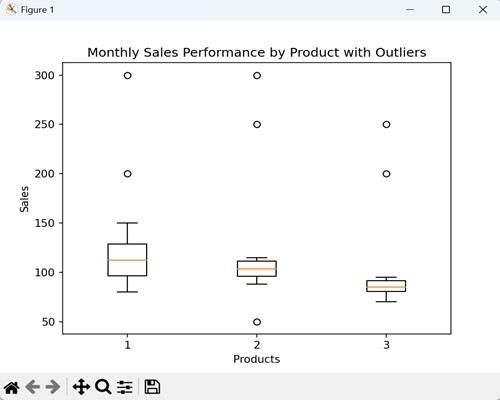
In the example below, we are creating a box plot that provides a visual representation of the sales distribution for each product, and the outliers highlight months with exceptionally high or low sales −

import matplotlib.pyplot as plt
import numpy as np

# Data for monthly sales
product_A_sales = [100, 110, 95, 105, 115, 90, 120, 130, 80, 125, 150, 200]
product_B_sales = [90, 105, 100, 98, 102, 105, 110, 95, 112, 88, 115, 250]
product_C_sales = [80, 85, 90, 78, 82, 85, 88, 92, 75, 85, 200, 95]

# Introducing outliers 
product_A_sales.extend([300, 80])
product_B_sales.extend([50, 300])
product_C_sales.extend([70, 250])

# Creating a box plot with outliers
plt.boxplot([product_A_sales, product_B_sales, product_C_sales], sym='o')
plt.title('Monthly Sales Performance by Product with Outliers')
plt.xlabel('Products')
plt.ylabel('Sales')
plt.show()

Output

On executing the above code we will get the following output −

Print Page