Matplotlib - 3D Wireframe Plots

---

---

A 3D wireframe plot is a way of representing data in three dimensions using lines to represent the shape of an object. A wireframe plot connects the data points of an object to create a mesh-like structure to show the shape of the object.

Imagine we have a cube and instead of drawing the solid faces of the cube, we only show the lines outlining its edges and corners. The outline we get is the 3D wireframe plot −

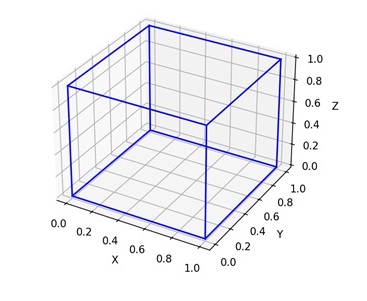
3D Wireframe Plot in Matplotlib

In Matplotlib, a 3D wireframe plot is a type of visualization where data is represented by a network of lines forming the edges of a three-dimensional surface.

We can create a 3D wireframe plot in Matplotlib using the plot_wireframe() function in the 'mpl_toolkits.mplot3d' module. This function accepts the X, Y, and Z coordinates of a 3D object and connects these coordinates with lines to create a 3D outline of the object.

Let’s start by drawing a basic 3D wireframe plot.

Basic 3D Wireframe Plot

A basic 3D wireframe plot in Matplotlib displays the surface of a 3D object as a mesh of lines, allowing you to visualize the shape and structure of the surface. The wireframe plot is formed by joining a series of points on the sphere's surface with straight lines running along the x, y, and z axes.

To create a wireframe plot, you can define arrays for the x, y, and z coordinates of the surface points you want to visualize. Then, you can pass these arrays to the plot_wireframe() function to generate the wireframe plot.

Example

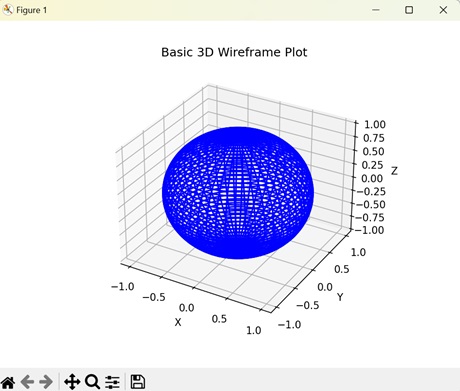
In the following example, we are creating a basic 3D wireframe plot of a spherical surface. First, we generate the X, Y, and Z points of the sphere by varying them with the angles 'theta' and 'phi'. Then, we use the plot_wireframe() function to create lines that connect the data points of the sphere. In the resultant plot, we get a 3D wireframe plot of a spherical surface −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Generating data for a spherical surface
theta = np.linspace(0, 2*np.pi, 100)
phi = np.linspace(0, np.pi, 100)
theta, phi = np.meshgrid(theta, phi)
r = 1
x = r * np.sin(phi) * np.cos(theta)
y = r * np.sin(phi) * np.sin(theta)
z = r * np.cos(phi)

# Creating a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plotting the spherical wireframe
ax.plot_wireframe(x, y, z, color='blue')

# Adding labels and title
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Basic 3D Wireframe Plot')

# Displaying the plot
plt.show()

Output

Following is the output of the above code −

Toroidal 3D Wireframe Plot

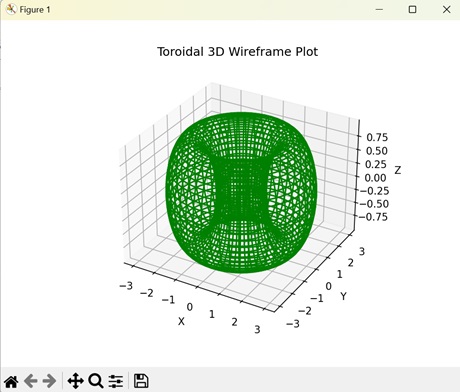
In Matplotlib, a toroidal 3D wireframe plot represents the surface of a torus using lines in three-dimensional space. A torus is a doughnut-shaped object with a hole in the middle. The wireframe plot connects the lines on surface of the torus to create its outline.

Example

In here, we are generating a toroidal 3D wireframe plot. We start by creating the surface of the torus by varying the X and Y coordinates with angles 'theta' and 'phi' and with major radius 'R' and minor radius 'r', while the Z coordinate varies with 'r' and 'phi'. Then, we use the plot_wireframe() function to connect the coordinates with lines creating a resultant plot which represents a 3D wireframe plot of a torus −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Generating data for a toroidal surface
theta = np.linspace(0, 2*np.pi, 100)
phi = np.linspace(0, 2*np.pi, 100)
theta, phi = np.meshgrid(theta, phi)
R = 2
r = 1
x = (R + r * np.cos(phi)) * np.cos(theta)
y = (R + r * np.cos(phi)) * np.sin(theta)
z = r * np.sin(phi)

# Creating a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plotting the toroidal wireframe
ax.plot_wireframe(x, y, z, color='green')

# Adding labels and title
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Toroidal 3D Wireframe Plot')

# Displaying the plot
plt.show()

Output

On executing the above code we will get the following output −

Paraboloid 3D Wireframe Plot

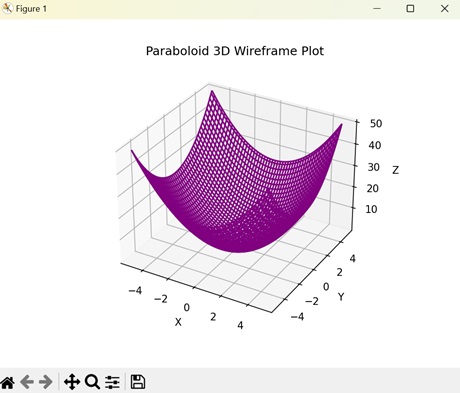
A paraboloid 3D wireframe plot in Matplotlib displays the outline of a paraboloid using lines on a three-dimensional graph. A paraboloid is a three-dimensional parabola that resembles a bowl. The 3D wireframe plot connects the data points to create a mesh-like structure of the paraboloid.

Example

The following example creates a 3D wireframe plot of a paraboloid in a 3D space. We create the paraboloid by evenly spacing the X, Y, and Z on a 3D graph. Then, we connect the coordinates with lines using the plot_wireframe() function to create a 3D wireframe plot −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Generating data for a paraboloid surface
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2

# Creating a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plotting the paraboloid wireframe
ax.plot_wireframe(X, Y, Z, color='purple')

# Adding labels and title
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Paraboloid 3D Wireframe Plot')

# Displaying the plot
plt.show()

Output

After executing the above code, we get the following output −

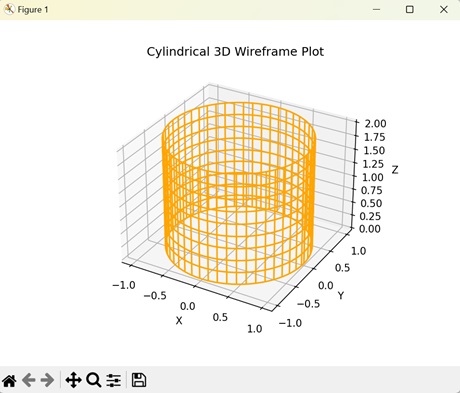
Cylindrical 3D Wireframe Plot

In Matplotlib, a cylindrical wireframe plot is a visualization of the geometry of a cylinder in a three-dimensional space. A cylinder is a three-dimensional shape with a circular cross-section that extends along its length. The data points on the surface of the cylinder are connected with lines to create a 3D wireframe plot.

Example

Now, we are generating a 3D wireframe plot for a cylinder on a 3D graph. We first plot the X and Y coordinates that represent the surface of the cylinder by varying them with the radius 'r' and the angle 'theta' (theta is in range 0 to 2π to cover a full circle). Then, we plot the Z coordinate that represents the height of the cylinder. After that, we use the plot_wireframe() function to join the coordinates with straight lines. This creates a resultant plot which shows the 3D wireframe plot of a cylinder −

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Defining the parameters
r = 1
h = 2
theta = np.linspace(0, 2*np.pi, 100)
z = np.linspace(0, h, 10)

# Generating cylinder coordinates
theta_3d, z_3d = np.meshgrid(theta, z)
x = r * np.cos(theta_3d)
y = r * np.sin(theta_3d)

# Creating a 3D plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plotting the cylindrical wireframe
ax.plot_wireframe(x, y, z_3d, color='orange')

# Adding labels and title
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Cylindrical 3D Wireframe Plot')

# Displaying the plot
plt.show()

Output

On executing the above code we will get the following output −