
- Machine Learning Basics
- Machine Learning - Home
- Machine Learning - Getting Started
- Machine Learning - Basic Concepts
- Machine Learning - Python Libraries
- Machine Learning - Applications
- Machine Learning - Life Cycle
- Machine Learning - Required Skills
- Machine Learning - Implementation
- Machine Learning - Challenges & Common Issues
- Machine Learning - Limitations
- Machine Learning - Reallife Examples
- Machine Learning - Data Structure
- Machine Learning - Mathematics
- Machine Learning - Artificial Intelligence
- Machine Learning - Neural Networks
- Machine Learning - Deep Learning
- Machine Learning - Getting Datasets
- Machine Learning - Categorical Data
- Machine Learning - Data Loading
- Machine Learning - Data Understanding
- Machine Learning - Data Preparation
- Machine Learning - Models
- Machine Learning - Supervised
- Machine Learning - Unsupervised
- Machine Learning - Semi-supervised
- Machine Learning - Reinforcement
- Machine Learning - Supervised vs. Unsupervised
- Machine Learning Data Visualization
- Machine Learning - Data Visualization
- Machine Learning - Histograms
- Machine Learning - Density Plots
- Machine Learning - Box and Whisker Plots
- Machine Learning - Correlation Matrix Plots
- Machine Learning - Scatter Matrix Plots
- Statistics for Machine Learning
- Machine Learning - Statistics
- Machine Learning - Mean, Median, Mode
- Machine Learning - Standard Deviation
- Machine Learning - Percentiles
- Machine Learning - Data Distribution
- Machine Learning - Skewness and Kurtosis
- Machine Learning - Bias and Variance
- Machine Learning - Hypothesis
- Regression Analysis In ML
- Machine Learning - Regression Analysis
- Machine Learning - Linear Regression
- Machine Learning - Simple Linear Regression
- Machine Learning - Multiple Linear Regression
- Machine Learning - Polynomial Regression
- Classification Algorithms In ML
- Machine Learning - Classification Algorithms
- Machine Learning - Logistic Regression
- Machine Learning - K-Nearest Neighbors (KNN)
- Machine Learning - Naïve Bayes Algorithm
- Machine Learning - Decision Tree Algorithm
- Machine Learning - Support Vector Machine
- Machine Learning - Random Forest
- Machine Learning - Confusion Matrix
- Machine Learning - Stochastic Gradient Descent
- Clustering Algorithms In ML
- Machine Learning - Clustering Algorithms
- Machine Learning - Centroid-Based Clustering
- Machine Learning - K-Means Clustering
- Machine Learning - K-Medoids Clustering
- Machine Learning - Mean-Shift Clustering
- Machine Learning - Hierarchical Clustering
- Machine Learning - Density-Based Clustering
- Machine Learning - DBSCAN Clustering
- Machine Learning - OPTICS Clustering
- Machine Learning - HDBSCAN Clustering
- Machine Learning - BIRCH Clustering
- Machine Learning - Affinity Propagation
- Machine Learning - Distribution-Based Clustering
- Machine Learning - Agglomerative Clustering
- Dimensionality Reduction In ML
- Machine Learning - Dimensionality Reduction
- Machine Learning - Feature Selection
- Machine Learning - Feature Extraction
- Machine Learning - Backward Elimination
- Machine Learning - Forward Feature Construction
- Machine Learning - High Correlation Filter
- Machine Learning - Low Variance Filter
- Machine Learning - Missing Values Ratio
- Machine Learning - Principal Component Analysis
- Machine Learning Miscellaneous
- Machine Learning - Performance Metrics
- Machine Learning - Automatic Workflows
- Machine Learning - Boost Model Performance
- Machine Learning - Gradient Boosting
- Machine Learning - Bootstrap Aggregation (Bagging)
- Machine Learning - Cross Validation
- Machine Learning - AUC-ROC Curve
- Machine Learning - Grid Search
- Machine Learning - Data Scaling
- Machine Learning - Train and Test
- Machine Learning - Association Rules
- Machine Learning - Apriori Algorithm
- Machine Learning - Gaussian Discriminant Analysis
- Machine Learning - Cost Function
- Machine Learning - Bayes Theorem
- Machine Learning - Precision and Recall
- Machine Learning - Adversarial
- Machine Learning - Stacking
- Machine Learning - Epoch
- Machine Learning - Perceptron
- Machine Learning - Regularization
- Machine Learning - Overfitting
- Machine Learning - P-value
- Machine Learning - Entropy
- Machine Learning - MLOps
- Machine Learning - Data Leakage
- Machine Learning - Resources
- Machine Learning - Quick Guide
- Machine Learning - Useful Resources
- Machine Learning - Discussion
Machine Learning - K-Medoids Clustering
K-Medoids Clustering - Algorithm
The K-medoids clustering algorithm can be summarized as follows −
Initialize k medoids − Select k random data points from the dataset as the initial medoids.
Assign data points to medoids − Assign each data point to the nearest medoid.
Update medoids − For each cluster, select the data point that minimizes the sum of distances to all the other data points in the cluster, and set it as the new medoid.
Repeat steps 2 and 3 until convergence or a maximum number of iterations is reached.
Implementation in Python
To implement K-medoids clustering in Python, we can use the scikit-learn library. The scikit-learn library provides the KMedoids class, which can be used to perform K-medoids clustering on a dataset.
First, we need to import the required libraries −
from sklearn_extra.cluster import KMedoids from sklearn.datasets import make_blobs import matplotlib.pyplot as plt
Next, we generate a sample dataset using the make_blobs() function from scikit-learn −
X, y = make_blobs(n_samples=500, centers=3, random_state=42)
Here, we generate a dataset with 500 data points and 3 clusters.
Next, we initialize the KMedoids class and fit the data −
kmedoids = KMedoids(n_clusters=3, random_state=42) kmedoids.fit(X)
Here, we set the number of clusters to 3 and use the random_state parameter to ensure reproducibility.
Finally, we can visualize the clustering results using a scatter plot −
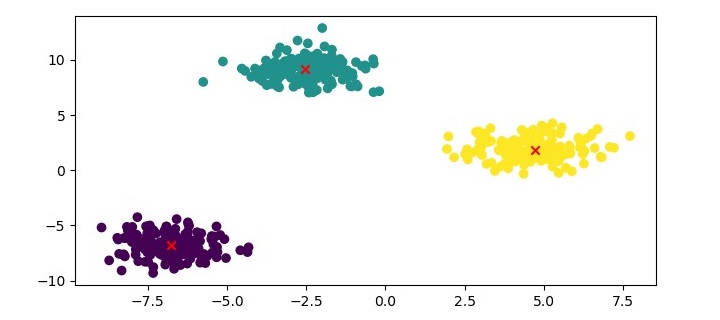
plt.figure(figsize=(7.5, 3.5)) plt.scatter(X[:, 0], X[:, 1], c=kmedoids.labels_, cmap='viridis') plt.scatter(kmedoids.cluster_centers_[:, 0], kmedoids.cluster_centers_[:, 1], marker='x', color='red') plt.show()
Example
Here is the complete implementation in Python −
from sklearn_extra.cluster import KMedoids from sklearn.datasets import make_blobs import matplotlib.pyplot as plt # Generate sample data X, y = make_blobs(n_samples=500, centers=3, random_state=42) # Cluster the data using KMedoids kmedoids = KMedoids(n_clusters=3, random_state=42) kmedoids.fit(X) # Plot the results plt.figure(figsize=(7.5, 3.5)) plt.scatter(X[:, 0], X[:, 1], c=kmedoids.labels_, cmap='viridis') plt.scatter(kmedoids.cluster_centers_[:, 0], kmedoids.cluster_centers_[:, 1], marker='x', color='red') plt.show()
Output
Here, we plot the data points as a scatter plot and color them based on their cluster labels. We also plot the medoids as red crosses.
K-Medoids Clustering - Advantages
Here are the advantages of using K-medoids clustering −
Robust to outliers and noise − K-medoids clustering is more robust to outliers and noise than K-means clustering because it uses a representative data point, called a medoid, to represent the center of the cluster.
Can handle non-Euclidean distance metrics − K-medoids clustering can be used with any distance metric, including non-Euclidean distance metrics, such as Manhattan distance and cosine similarity.
Computationally efficient − K-medoids clustering has a computational complexity of O(k*n^2), which is lower than the computational complexity of K-means clustering.
K-Medoids Clustering - Disadvantages
The disadvantages of using K-medoids clustering are as follows −
Sensitive to the choice of k − The performance of K-medoids clustering can be sensitive to the choice of k, the number of clusters.
Not suitable for high-dimensional data − K-medoids clustering may not perform well on high-dimensional data because the medoid selection process becomes computationally expensive.