Machine Learning - DBSCAN Clustering

The DBSCAN Clustering algorithm works as follows −

Randomly select a data point that has not been visited.
If the data point has at least minPts neighbors within distance eps, create a new cluster and add the data point and its neighbors to the cluster.
If the data point does not have at least minPts neighbors within distance eps, mark the data point as noise and continue to the next data point.
Repeat steps 1-3 until all data points have been visited.

Implementation in Python

We can implement the DBSCAN algorithm in Python using the scikit-learn library. Here are the steps to do so −

Load the dataset

The first step is to load the dataset. We will use the make_moons function from the scikitlearn library to generate a toy dataset with two moons.

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)

Perform DBSCAN clustering

The next step is to perform DBSCAN clustering on the dataset. We will use the DBSCAN class from the scikit-learn library. We will set the minPts parameter to 5 and the "eps" parameter to 0.2.

from sklearn.cluster import DBSCAN
clustering = DBSCAN(eps=0.2, min_samples=5)
clustering.fit(X)

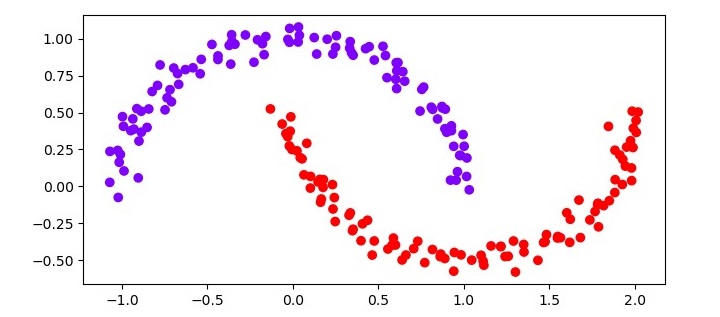
Visualize the results

The final step is to visualize the results of the clustering. We will use the Matplotlib library to create a scatter plot of the dataset colored by the cluster assignments.

import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_, cmap='rainbow')
plt.show()

Example

Here is the complete implementation of DBSCAN clustering in Python −

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
from sklearn.cluster import DBSCAN

clustering = DBSCAN(eps=0.2, min_samples=5)
clustering.fit(X)

import matplotlib.pyplot as plt
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], c=clustering.labels_, cmap='rainbow')

plt.show()

Output

The resulting scatter plot should show two distinct clusters, each corresponding to one of the moons in the dataset. The noise data points should be colored black.

Advantages of DBSCAN

Following are the advantages of using DBSCAN clustering −

DBSCAN can handle clusters of arbitrary shape, unlike k-means, which assumes that clusters are spherical.
It does not require prior knowledge of the number of clusters in the dataset, unlike k-means.
It can detect outliers, which are points that do not belong to any cluster. This is because DBSCAN defines clusters as dense regions of points, and points that are far from any dense region are considered outliers.
It is relatively insensitive to the initial choice of parameters, such as the epsilon and min_samples parameters, unlike k-means.
It is scalable to large datasets, as it only needs to compute pairwise distances between neighboring points, rather than all pairs of points.

Disadvantages of DBSCAN

Following are the disadvantages of using DBSCAN clustering −

It can be sensitive to the choice of the epsilon and min_samples parameters. If these parameters are not chosen carefully, DBSCAN may fail to identify clusters or merge them incorrectly.
It may not work well on datasets with varying densities, as it assumes that all clusters have the same density.
It may produce different results for different runs on the same dataset, due to the non-deterministic nature of the algorithm.
It may be computationally expensive for high-dimensional datasets, as the distance computations become more expensive as the number of dimensions increases.
It may not work well on datasets with noise or outliers if the density of the noise or outliers is too high. In such cases, the noise or outliers may be wrongly assigned to clusters.

Print Page