
- C Programming Tutorial
- C - Home
- Basics of C
- C - Overview
- C - Features
- C - History
- C - Environment Setup
- C - Program Structure
- C - Hello World
- C - Compilation Process
- C - Comments
- C - Tokens
- C - Keywords
- C - Identifiers
- C - User Input
- C - Basic Syntax
- C - Data Types
- C - Variables
- C - Integer Promotions
- C - Type Conversion
- C - Type Casting
- C - Booleans
- Constants and Literals in C
- C - Constants
- C - Literals
- C - Escape sequences
- C - Format Specifiers
- Operators in C
- C - Operators
- C - Arithmetic Operators
- C - Relational Operators
- C - Logical Operators
- C - Bitwise Operators
- C - Assignment Operators
- C - Unary Operators
- C - Increment and Decrement Operators
- C - Ternary Operator
- C - sizeof Operator
- C - Operator Precedence
- C - Misc Operators
- Decision Making in C
- C - Decision Making
- C - if statement
- C - if...else statement
- C - nested if statements
- C - switch statement
- C - nested switch statements
- Loops in C
- C - Loops
- C - While loop
- C - For loop
- C - Do...while loop
- C - Nested loop
- C - Infinite loop
- C - Break Statement
- C - Continue Statement
- C - goto Statement
- Functions in C
- C - Functions
- C - Main Function
- C - Function call by Value
- C - Function call by reference
- C - Nested Functions
- C - Variadic Functions
- C - User-Defined Functions
- C - Callback Function
- C - Return Statement
- C - Recursion
- Scope Rules in C
- C - Scope Rules
- C - Static Variables
- C - Global Variables
- Arrays in C
- C - Arrays
- C - Properties of Array
- C - Multi-Dimensional Arrays
- C - Passing Arrays to Function
- C - Return Array from Function
- C - Variable Length Arrays
- Pointers in C
- C - Pointers
- C - Pointers and Arrays
- C - Applications of Pointers
- C - Pointer Arithmetics
- C - Array of Pointers
- C - Pointer to Pointer
- C - Passing Pointers to Functions
- C - Return Pointer from Functions
- C - Function Pointers
- C - Pointer to an Array
- C - Pointers to Structures
- C - Chain of Pointers
- C - Pointer vs Array
- C - Character Pointers and Functions
- C - NULL Pointer
- C - void Pointer
- C - Dangling Pointers
- C - Dereference Pointer
- C - Near, Far and Huge Pointers
- C - Initialization of Pointer Arrays
- C - Pointers vs. Multi-dimensional Arrays
- Strings in C
- C - Strings
- C - Array of Strings
- C - Special Characters
- C Structures and Unions
- C - Structures
- C - Structures and Functions
- C - Arrays of Structures
- C - Self-Referential Structures
- C - Lookup Tables
- C - Dot (.) Operator
- C - Enumeration (or enum)
- C - Structure Padding and Packing
- C - Nested Structures
- C - Anonymous Structure and Union
- C - Unions
- C - Bit Fields
- C - Typedef
- File Handling in C
- C - Input & Output
- C - File I/O (File Handling)
- C Preprocessors
- C - Preprocessors
- C - Pragmas
- C - Preprocessor Operators
- C - Macros
- C - Header Files
- Memory Management in C
- C - Memory Management
- C - Memory Address
- C - Storage Classes
- Miscellaneous Topics
- C - Error Handling
- C - Variable Arguments
- C - Command Execution
- C - Math Functions
- C - Static Keyword
- C - Random Number Generation
- C - Command Line Arguments
- C Programming Resources
- C - Questions & Answers
- C - Quick Guide
- C - Cheat Sheet
- C - Useful Resources
- C - Discussion
Multi-dimensional Arrays in C
The array is declared with one value of size in square brackets, it is called one dimensional array. In a one dimensional array, each element is identified by its index or subscript. In C, you can declare with more indices to simulate a two, three or multidimensional array.
Multidimensional Arrays in C
Multi-dimensional arrays can be termed as nested arrays. In such a case, each element in the outer array is an array itself. Such type of nesting can be upto any level. If each element in the outer array is another one-dimensional array, it forms a two-dimensional array. In turn, the inner array is an array of another set of one dimensional array, it is a three-dimensional array, and so on.
Declaration of Multidimensional Arrays
Depending on the nesting level, the multi-dimensional array is declared as follows −
type name[size1][size2]...[sizeN];
For example, the following declaration creates a three dimensional integer array −
int threedim[3][3][3];
A multidimensional array can have any number of dimensions. In this tutorial, we will learn about the two commonly used types of multidimensional arrays:
- Two-dimensional Array
- Three-dimensional Array
Two-dimensional Array in C
A two-dimensional array in an array of one-dimensional arrays. Each element of a two-dimensional array is an array itself. It is like a table or a matrix. The elements can be considered to be logically arranged in rows and columns. Hence, the location of any element is characterised by its row number and column number. Both row and column index start from 0.
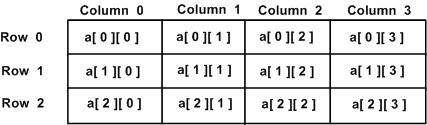
Declaration and Initialization of Two-dimensional Array
The following statement declares and initializes a two-dimensional array −
int arr[3][5] = {1,2,3,4,5, 10,20,30,40,50, 5,10,15,20,25};
The arr array has three rows and five columns. In C, a two dimensional array is a row−major array. The first square bracket always represents the dimension size of rows, and the second is the number of columns. Obviously, the array has 3 X 5 = 15 elements. The array is initialized with 15 comma−separated values put inside the curly brackets.
Elements are read into the array in a row−wise manner, which means the first 5 elements are stored in first row, and so on. Hence, the first dimension is optional in the array declaration.
int arr[ ][5] = {1,2,3,4,5, 10,20,30,40,50, 5,10,15,20,25};
To increase the readability, elements of each row can be optionally put in curly brackets as follows −
int arr[ ][5] = {
{1,2,3,4,5},
{10,20,30,40,50},
{5,10,15,20,25}
};
The numbers are logically arranged in a tabular manner as follows −
| 1 | 2 | 3 | 4 | 5 |
| 10 | 20 | 30 | 40 | 50 |
| 5 | 10 | 15 | 20 | 25 |
The cell with row index 1 and column index 2 has 30 in it.
Example of Printing Elements of Two-dimensional Array
The program below displays the row and column indices of each element in a 2D array −
#include <stdio.h>
int main () {
/* an array with 5 rows and 2 columns*/
int a[5][2] = { {0,0}, {1,2}, {2,4}, {3,6},{4,8}};
int i, j;
/* output each array element's value */
for ( i = 0; i < 5; i++ ) {
for ( j = 0; j < 2; j++ ) {
printf("a[%d][%d] = %d\n", i,j, a[i][j] );
}
}
return 0;
}
Output
a[0][0] = 0 a[0][1] = 0 a[1][0] = 1 a[1][1] = 2 a[2][0] = 2 a[2][1] = 4 a[3][0] = 3 a[3][1] = 6 a[4][0] = 4 a[4][1] = 8
In case of a two or multi-dimensional array, the compiler assigns a memory block of the size which is the product of dimensions multiplied by the size of the data type. In this case, the size is 3 X 5 X 4 = 60 bytes, 4 being the size of int data type.
Even though all the elements are stored in consecutive memory locations, we can print the elements in row and column format with the use of nested loops.
Example of Printing Two-dimensional Array as Matrix in Row and Columns
The following program prints a two-dimensional array in row and columns.
#include <stdio.h>
int main() {
int arr[3][5] = {1,2,3,4,5, 10,20,30,40,50, 5,10,15,20,25};
int i, j;
for (i=0; i<3; i++){
for (j=0; j<5; j++){
printf("%4d", arr[i][j]);
}
printf("\n");
}
return 0;
}
Output
1 2 3 4 5 10 20 30 40 50 5 10 15 20 25
Three-dimensional Array in C
A three-dimensional array is an array of two-dimensional arrays, where each element is a two-dimensional array. A 3D array needs three subscripts to define depth, row, and column.
Imagine the students appearing for an exam are seated in five halls, each hall having twenty rows of desks, and each row has 5 tables. Such an arrangement is represented by a three dimensional array such as −
Students[hall][row][column]
To locate each student, you need to have three indices, hall number, row and column of his table in the hall.
Example of Three-dimensional Array
The following program stores numbers in a 3 X 3 X 3 array −
#include<stdio.h>
int main(){
int i, j, k;
int arr[3][3][3]= {
{
{11, 12, 13},
{14, 15, 16},
{17, 18, 19}
},
{
{21, 22, 23},
{24, 25, 26},
{27, 28, 29}
},
{
{31, 32, 33},
{34, 35, 36},
{37, 38, 39}
},
};
printf("Printing 3D Array Elements\n");
for(i=0;i<3;i++) {
for(j=0;j<3;j++){
for(k=0;k<3;k++){
printf("%4d",arr[i][j][k]);
}
printf("\n");
}
printf("\n");
}
return 0;
}
Output
Printing 3D Array Elements 11 12 13 14 15 16 17 18 19 21 22 23 24 25 26 27 28 29 31 32 33 34 35 36 37 38 39
Row-wise Sum of Multidimensional Array's Elements
You can find the sum of all elements row-wise or column-wise by accessing the elements using indices. In the case of a three-dimensional array, you need to use depth, row, and column indices. And, in the case of a two-dimensional array, you need to use row and column indices. Here, we are using a two-dimensional array.
Example: Row-wise Sum of Numbers
In the following program, sum of integer elements in each row of a two-dimensional array is displayed.
#include <stdio.h>
int main() {
int arr[3][5] = {{1,2,3,4,5}, {10,20,30,40,50}, {5,10,15,20,25}};
int i, j;
int sum;
for (i=0; i<3; i++){
sum=0;
for (j=0; j<5; j++){
sum+=arr[i][j];
}
printf("Sum of row %d: %d\n", i, sum);
}
return 0;
}
Output
Sum of row 0: 15 Sum of row 1: 150 Sum of row 2: 75
Matrix Multiplication
Matrix algebra is a branch of mathematics, where a matrix is a 2D array of numbers arranged in rows and columns. Multiplication of two matrices is possible only if the number of columns of the first matrix is equal to the number of rows of the second matrix. The product of two compatible matrices is equal to the dot products between rows of the first matrix and columns of the second matrix.
If the two matrices are of size a[m][n] and b[p][q], the result of their multiplication is a matrix of the size (the multiplication is possible only if n is equal to p) is c[m][q].
The product of two matrices, is the sum of the products across some row of matrix A with the corresponding entries down some column of matrix B.
Example of Multiplication of Two-dimensional Array (Matrix)
The following program performs the multiplication of two matrices.
#include<stdio.h>
int main(){
int mat1[3][3] = { {2, 4, 1} , {2, 3, 9} , {3, 1, 8} };
int mat2[3][3] = { {1, 2, 3} , {3, 6, 1} , {2, 4, 7} };
int mat3[3][3], sum=0, i, j, k;
for(i=0; i<3; i++){
for(j=0; j<3; j++){
sum=0;
for(k=0; k<3; k++)
sum = sum + mat1[i][k] * mat2[k][j];
mat3[i][j] = sum;
}
}
printf("\nMatrix 1 ...\n");
for(i=0; i<3; i++){
for(j=0; j<3; j++)
printf("%d\t", mat1[i][j]);
printf("\n");
}
printf("\nMatrix 2 ...\n");
for(i=0; i<3; i++){
for(j=0; j<3; j++)
printf("%d\t", mat2[i][j]);
printf("\n");
}
printf("\nMultiplication of the two given Matrices: \n");
for(i=0; i<3; i++){
for(j=0; j<3; j++)
printf("%d\t", mat3[i][j]);
printf("\n");
}
return 0;
}
Output
Matrix 1 ... 2 4 1 2 3 9 3 1 8 Matrix 2 ... 1 2 3 3 6 1 2 4 7 Multiplication of the two given Matrices: 16 32 17 29 58 72 22 44 66
